RC Circuit Reduction

RC Circuit Reduction#

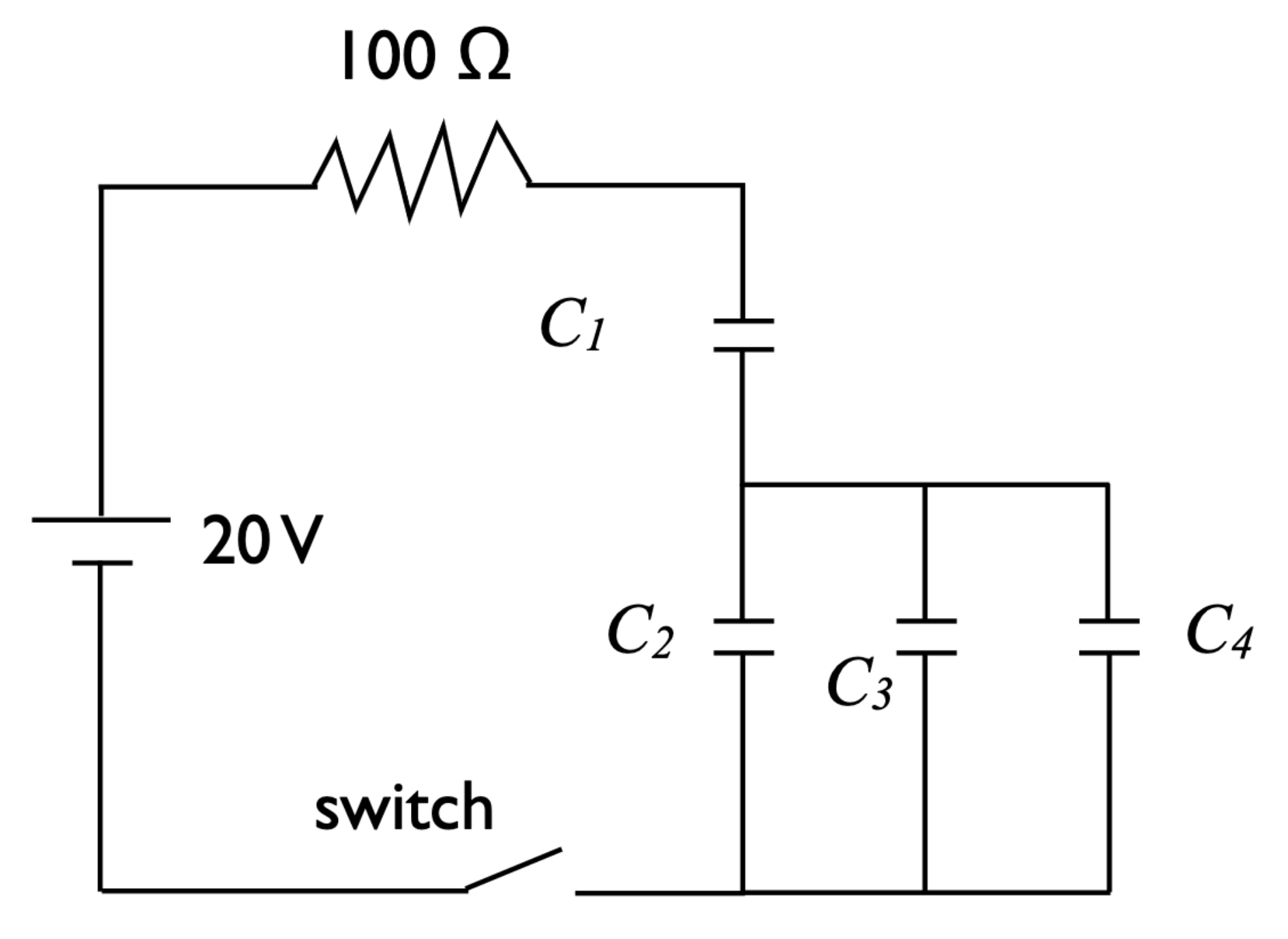
Consider the RC circuit shown below. Here, \(C_1 = {{ params.c1 }}\) \(\rm{\mu F}\), \(C_2 = {{ params.c2 }}\) \(\rm{\mu F}\), \(C_3 = {{ params.c3 }}\) \(\rm{\mu F}\), and \(C_4 = {{ params.c4 }}\) \(\rm{\mu F}\).

In this problem we will find the equivalent capacitance of this capacitor system in two steps. We will then use this result to determine the carge stored in the capacitor system.

A circuit diagram showing a 20 volt battery with its long teminal connected to a 100 ohm resistor that is connected to a capacitor with capacitance C1. After the capacitor, the circuit splits into three paths. One is connected to a capacitor with capacitance C2, another is connected to a capacitor with capacitance C3, and another is connected to a capacitor with capacitance C4. The paths then come together and connect to a switch, which is connected back to the short terminal the battery.

Part 1#

Select the capacitors that are in parallel with eachother.

Answer Section#

  • \(C_1\)

  • \(C_2\)

  • \(C_3\)

  • \(C_4\)

Part 2#

Redraw the circuit by replacing the capacitors that you identified in Part 1 by an equivalent capacitor with capacitance \(C_5\). Determine value of \(C_5\).

Round your answer to three significant figures.

Answer Section#

Please enter an answer in \(\rm{\mu F}\).

Part 3#

For your redrawn circuit, select the capacitors that are in series with each other. Do not select any capacitors that you have replaced.

Answer Section#

  • \(C_1\)

  • \(C_2\)

  • \(C_3\)

  • \(C_4\)

  • \(C_5\)

Part 4#

Redraw the circuit by replacing the capacitors that you identified in Part 3 by an equivalent capacitor with capacitance \(C_6\). Determine the value of \(C_6\).

Round your answer to three significant figures.

Answer Section#

Please enter an answer in \(\rm{\mu F}\).

Part 5#

Find the time constant \(\tau\) for this circuit.

Round your answer to three significant figures.

Answer Section#

Please enter an answer in \(\rm{s}\).

Part 6#

Find the maximum charge \(Q\) that can be stored in this capacitor system.

Answer Section#

Please enter an answer in \(\rm{C}\).

Attribution#

Problem is licensed under the CC-BY-NC-SA 4.0 license.
The Creative Commons 4.0 license requiring attribution-BY, non-commercial-NC, and share-alike-SA license.