Rotation on a Frictionless Table#
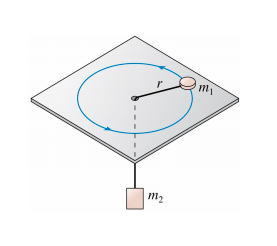
A mass \(m_1\) is connected to a mass \(m_2\) by a massless string that passes through a hole in a table as shown in the figure below. Mass \(m_1\) rotates about the hole with radius \(r\), while mass \(m_2\) hangs below the table. The angular velocity \(\omega\) of mass \(m_1\) is such that \(m_2\) remains at rest.
Part 1#
What is the centripital force \(F_c\) acting on mass \(m1\)?
Note that it may not be necessary to use every variable. Use the following table as a reference for each variable:
For |
Use |
|---|---|
\(m_1\) |
m1 |
\(m_2\) |
m2 |
\(g\) |
g |
\(r\) |
r |
Answer Section#
Part 2#
What is the velocity of mass \(m_1\)?
Note that it may not be necessary to use every variable. Use the following table as a reference for each variable:
For |
Use |
|---|---|
\(m_1\) |
m1 |
\(m_2\) |
m2 |
\(g\) |
g |
\(r\) |
r |
Answer Section#
Part 3#
What is the angular velocity of mass \(m1\)?
Note that it may not be necessary to use every variable. Use the following table as a reference for each variable:
For |
Use |
|---|---|
\(m_1\) |
m1 |
\(m_2\) |
m2 |
\(g\) |
g |
\(r\) |
r |
Answer Section#
Attribution#
Problem is licensed under the CC-BY-NC-SA 4.0 license.

