Stationary Pulley

Stationary Pulley#

A mass on a frictionless inclined plane \(m = {{ params.m }} \rm{kg}\) is connected to a pulley by a massless string at an inner radius \(r_i = {{params.ri}} \rm{cm}\). Another mass \(M\) is hanging from the pulley by a massless string connected at an outer radius \(r_o = {{ params.ro }} \rm{cm}\). The inclined plane makes an angle \(\theta = {{ prams.theta }}^\circ\) with the horizontal.

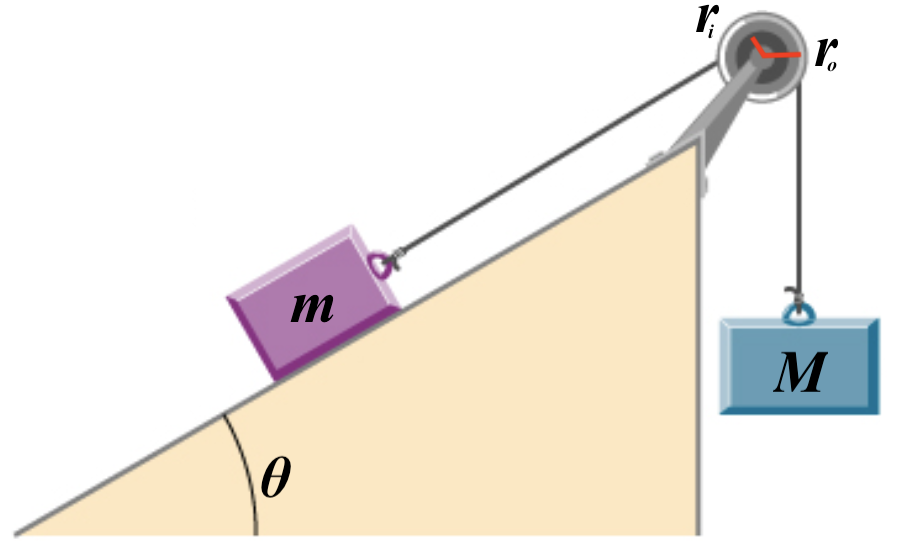
An image of a frictionless inclined plane with a pulley at its upper end. A mass on the plane is connected to the pulley by a massless string at the inner radius of the pulley. Another mass is hanging from the pulley by a massless string connected at the outer radius of the pulley.

Part 1#

What must the hanging mass \(M\) be to keep the pulley from rotating?

Answer Section#

Please enter a numeric value in \(\rm{kg}\).

Attribution#

Problem is from the OpenStax University Physics Volume 1 textbook, licensed under the CC-BY 4.0 license.
Image representing the Creative Commons 4.0 BY license.