Time Dependent Magnetic Field#
Part 1#
A rectangular wire loop with length \(a\) and width \(b\) lies in the xy-plane, as shown below. Within the loop there is a time-dependent magnetic field given in the figure below in units of tesla. Determine the emf induced in the loop as a function of time.
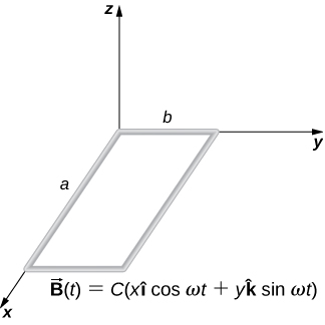
Answer Section#
\(\frac{-Cab^2{\omega}}{2}\)cos(\({\omega}t\))
\(\frac{Cab^2{\omega}}{2}\)cos(\({\omega}t\))
\(\frac{-Cab^2{\omega}}{2}\)sin(\({\omega}t\))
\(\frac{Cab^2{\omega}}{2}\)sin(\({\omega}t\))
\(-Cab{\omega}\)sin(\({\omega}t\))
Attribution#
Problem is from the OpenStax University Physics Volume 2 textbook, licensed under the CC-BY 4.0 license.
