Folding Platform#
A platform of length \(x = {{params.x}}\ \rm{m}\) is being folded up against a wall by a rope pulling on its end. The rope is retracting at a constant rate of \(\dot{\ell} = {{params.l_dot}}\ \rm{m/s}\). The distance between the pivot and where the rope is pulling from is \(h = {{params.h}}\ \rm{m}\).
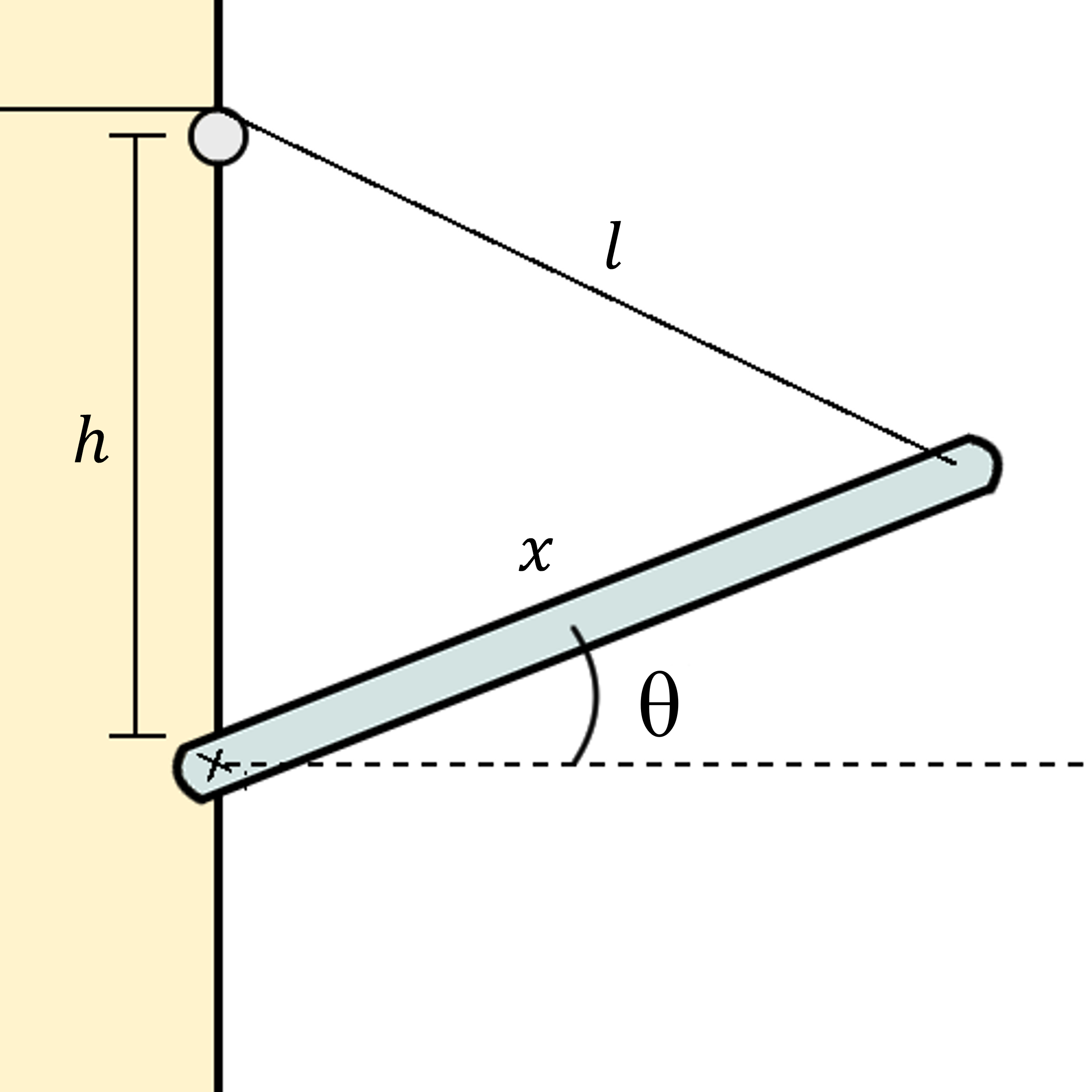
Part 1#
When \(\theta = {{params.theta}}^{\circ}\), what is \(\dot{\theta}\)?
Answer Section#
Please enter in a numeric value in \(/s\).
Part 2#
What is \(\ddot{\theta}\)?
Answer Section#
Please enter in a numeric value in \(/s^2\).
Attribution#
Problem is licensed under the CC-BY-NC-SA 4.0 license.

