Kinetic energy from velocity in SHM

Contents

Kinetic energy from velocity in SHM#

Part 1#

For a simple harmonic oscillator with velocity \(v_x(t) = v\_{max}\sin(\frac{2\pi t}{12} - \frac{\pi}{3})\), find the period of oscillation of the velocity.

Answer Section#

Please enter in a numeric value in \(rm\{s}\).

Part 2#

Identify which of the below graphs represents the kinetic energy as a function of time for a simple harmonic oscillator with velocity \(v_x(t) = v\_{max}\sin(\frac{2\pi t}{12} - \frac{\pi}{3})\).

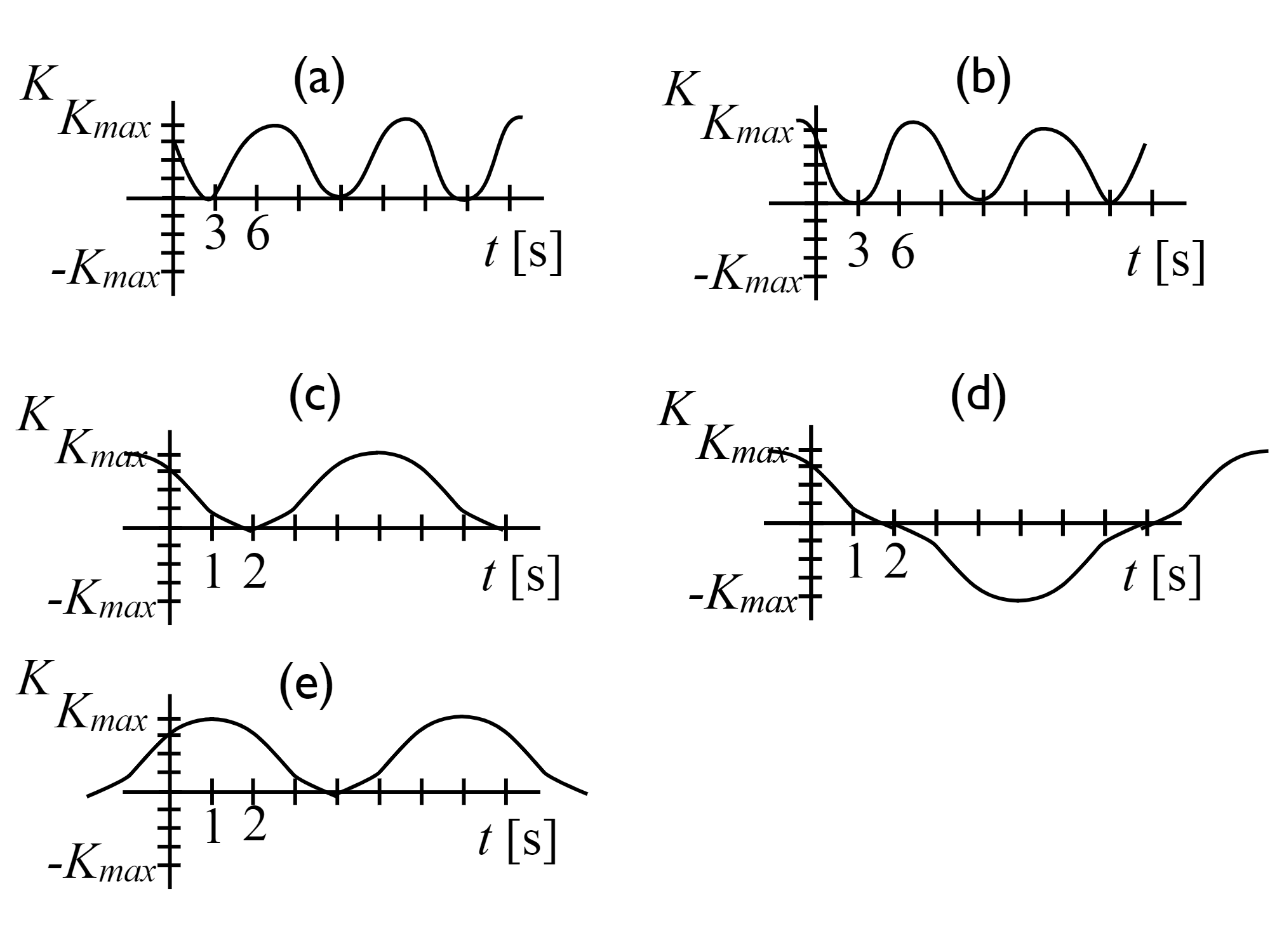
Image of five graphs. The five graphs represent the kinetic energy as a function of time for a simple harmonic oscillator. Graph A shows positive kinetic energy at all times with K = 0 at t = 1s. Graph B shows positive kinetic energy at all times with K = 0 at t = 1s. Graph C shows positive kinetic energy at all times with K = 0 at t = 2s. Graph D shows negative kinetic energy at 2s < t < 8s with K = 0 at t = 2s and t = 8s. Graph E shows positive kinetic energy at all times with K = 0 at t = 4s.

Answer Section#

Figure A
Figure B
Figure C
Figure D
Figure E

Attribution#

Problem is licensed under the CC-BY-NC-SA 4.0 license.
The Creative Commons 4.0 license requiring attribution-BY, non-commercial-NC, and share-alike-SA license.