Speed of a Rolling Object

Consider the setup shown in the figure below. One end of a string of negligible mass is connected to a round object of mass \(m\) and circular cross-section of radius \(r\). The string is connected to the round object via a frictionless axel of negligible mass that passes through the centre of mass of the round object. The round object is on an incline that makes an angle \(\theta = 30^{\circ}\) with the horizontal. The string runs over a frictionless pulley of negligible mass and the other end of the string is connected to a rectangular object of mass \(m\). The pulley is positioned at the end of the incline such that the rectangular object is suspended in the air.

The system is initally at rest, but once the rectangular object is released, it accelerates downward, causing the round object to roll up the incline without slipping. Find the speed of the round object when the rectangular object has fallen \(h =\) 11.6 \(\rm{m}\) for the case where the round object is a solid sphere, hollow sphere, or a solid cylinder.

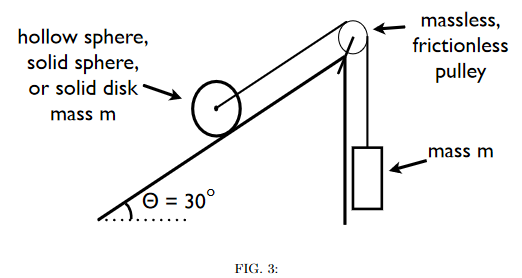
Long Description of Image: Figure of the system described in the question text.

A round object rolls up an incline. The round object is attached to a string which passes over a frictionless pulley of negligible mass positioned at the end of the incline. A rectangular object is suspended from the opposite end of the string.

Long description ends.

Part 1

Find the speed of the round object assuming that it is a solid sphere.

Answer Section

Please enter in a numeric value in \( m{m/s}\).

Part 2

Find the speed of the round object assuming that it is a hollow sphere.

Answer Section

Please enter in a numeric value in \( m{m/s}\).

Part 3

Find the speed of the round object assuming that it is a solid cylinder.

Answer Section

Please enter in a numeric value in \( m{m/s}\).

Attribution

Problem is licensed under the CC-BY-NC-SA 4.0 license.