A Frictionless Air Track?

A Frictionless Air Track?#

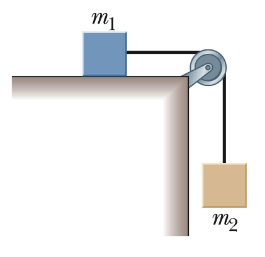
Because of Mateo’s excellent work in lab, their professor asks them to test out a new “frictionless” air track, which can be used to measure the acceleration due to gravity. In Mateo’s setup, they place a cart with mass \(m_1\) = 456.9 \(g\) on the track and suspend a second mass \(m_2\) = 43.86 \(g\) over a (supposedly) massless, frictionless pulley. Using a photogate that reads the acceleration of the system at the pulley, Mateo measures the acceleration in 10 trials as given in the table below. The uncertainty in each acceleration measurement is \(\pm\) 0.02 \(m/s^2\); the uncertainties in \(m_1\) and \(m_2\) are negligible. The mean and standard deviation (SD) of the acceleration data are also given in the table. Given these data, would you conclude that the air track system is frictionless as claimed? Justify your answer!

Mass m one sits on a horizontal surface while mass m two is suspended over a pulley. The masses are connected by a string.

Trial

Accel. (\(m/s^2\))

1

1.64

2

1.31

3

1.52

4

1.58

5

1.72

6

1.61

7

1.48

8

1.72

9

1.45

10

1.34

Mean

1.54

SD

0.136

Part 1#

Calculate \(a\_{expected}\).

Answer Section#

Please enter in a numeric value in \(m/s^2\).

Part 2#

Calculate \(a\_{measured}\).

Answer Section#

Please enter in a numeric value in \(m/s^2\).

Part 3#

Calculate the standard error of \(a\_{measured}\).

Answer Section#

Please enter in a numeric value in \(m/s^2\).

Part 4#

Would you conclude that the air track system is frictionless as claimed? Justify your answer!

Answer Section#

  • The track is frictionless because \(a_{expected}\) does not agree with \(a_{measured}\).

  • The track is not frictionless because \(a_{expected}\) agrees with \(a_{measured}\).

  • The track is not frictionless because \(a_{expected}\) does not agree with \(a_{measured}\).

  • The track is frictionless because \(a_{expected}\) agrees with \(a_{measured}\).

Attribution#

Problem is licensed under the CC-BY-NC-SA 4.0 license.
The Creative Commons 4.0 license requiring attribution-BY, non-commercial-NC, and share-alike-SA license.