Golf Ball in Hole

Golf Ball in Hole#

A golf ball lands with a speed of \(u = {{ params.u }}\ \rm{m/s}\) in a tapered frictionless hole as shown below.

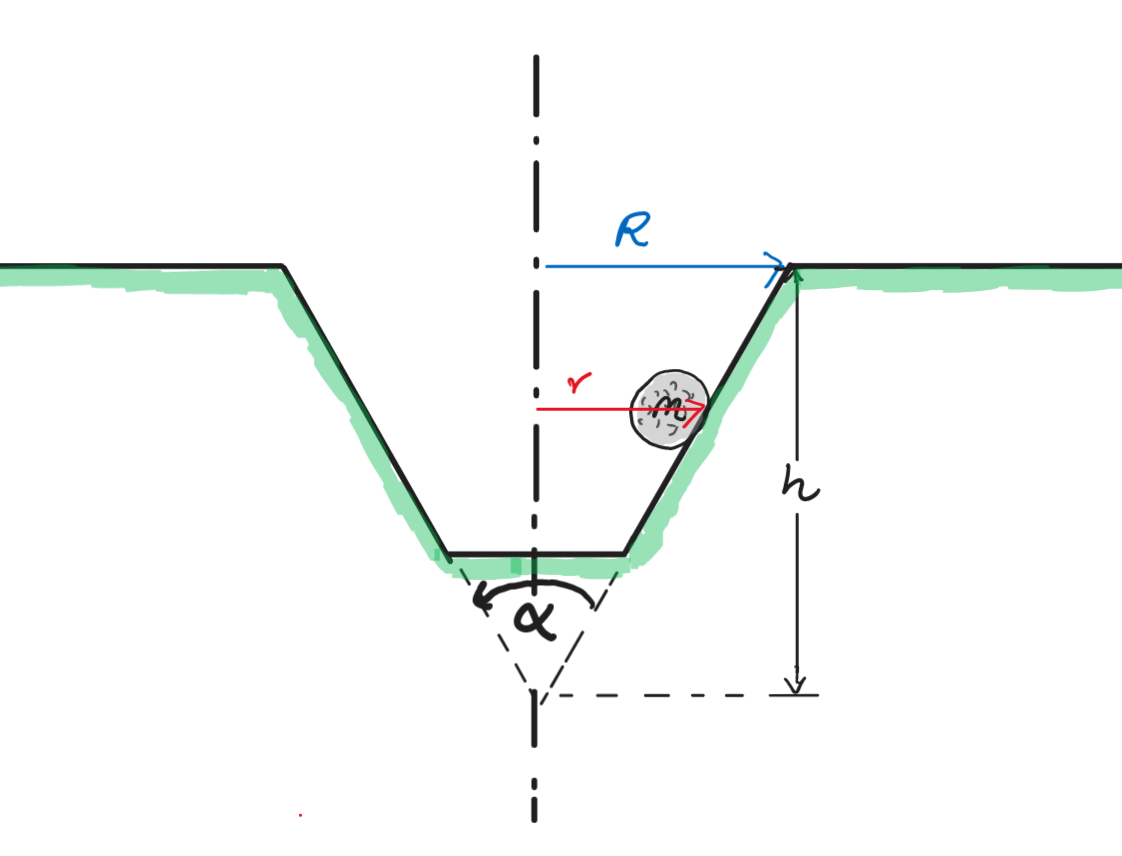
../../../../../_images/part119.png

Part 1#

Does the golf ball remain in stable orbit at the circle of radius \(r\), if the ball begins to rotate about the vertical axis of the hole at point A?
\(r = {{ params.r }}\ \rm{m}\), \(\alpha = {{ params.a }}^{\circ}\)

Answer Section#

  • True

  • False

Part 2#

Determine the maximum speed of the ball for it to remain in stable orbit about the circle of radius \(r\).

Answer Section#

Please enter a value in \(m/s\).

Part 3#

Using principles of conservation of energy, does the ball spin out of the hole?
\(H\_{hole} = {{ params.h }}\ \rm{m}\), \(R\_{hole}= {{ params.r_h }}\ \rm{m}\).

Answer Section#

  • No

  • Yes

Part 4#

Determine the radius of the stable orbit gained by the golf ball(i.e stable implies that the centripetal force is sufficiently provided by the forces acting on the ball and the ball rotates in a circle of constant height).

Answer Section#

Please enter a value in \(m\).

Part 5#

What is the speed of the golf ball in this stable orbit?

Answer Section#

Please enter a value in \(m/s\).

Attribution#

Problem is licensed under the CC-BY-NC-SA 4.0 license.
The Creative Commons 4.0 license requiring attribution-BY, non-commercial-NC, and share-alike-SA license.