Position Graph

Position Graph#

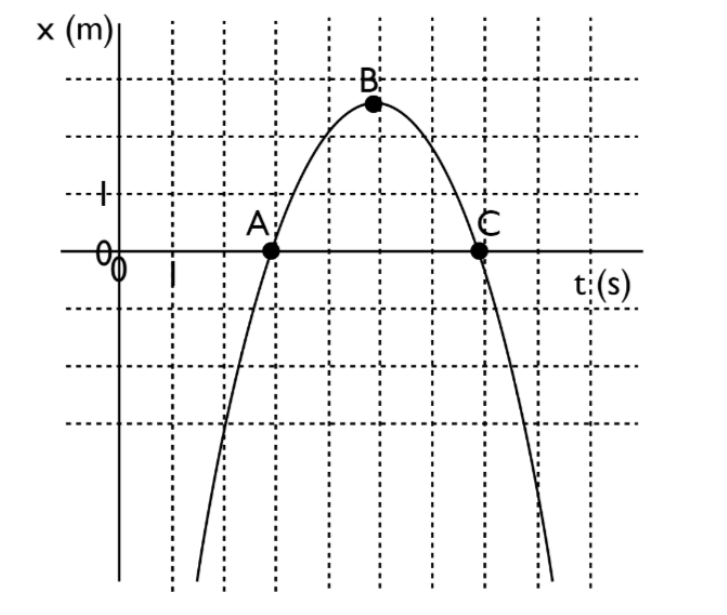
At each of A, B and C on the graph below, estimate the \(x\)-component of the velocity vector, \(v_x\) from the position vs. time graph.

This is a position vs. time graph. The y-axis is labelled 'x (m)' and the x-axis is labelled 't (s)'. Each grid is 1m and 1s. There is an upside down parabola, with its roots at t = 3s (labelled point A) and 7s (labelled point C). Its vertex is approximately at 2.5m and 5s (labelled point B). The rest of the parabola extends downwards to infinity.

Part 1#

Draw a tangent line to the graph at each point (A,B,C).

Please save the above image to use for sketching on the graph. Make sure to keep your tangent lines clear.

Upload your final graph as a pdf file titled “graph.pdf”.

Answer Section#

File upload box will be shown here.

Part 2#

Please enter your estimation of the \(x\)-component of the velocity vector \(v_x\) at A.

Answer Section#

Please enter in a numeric value.

Part 3#

Please enter your estimation of the \(x\)-component of the velocity vector \(v_x\) at B.

Answer Section#

Please enter in a numeric value.

Part 4#

Please enter your estimation of the \(x\)-component of the velocity vector \(v_x\) at C.

Answer Section#

Please enter in a numeric value.

Part 5#

What sign, if any, does the x-component of the acceleration vector, \(a_x\) , have at point B?

Answer Section#

Attribution#

Problem is licensed under the CC-BY-NC-SA 4.0 license.
The Creative Commons 4.0 license requiring attribution-BY, non-commercial-NC, and share-alike-SA license.