Box on a Slant with a Pulley#
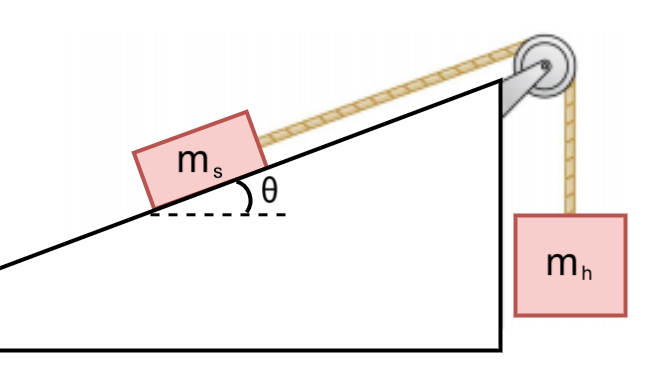
The figure shows a block of mass \(m_s\) resting on a \(\theta = {{params.angl}}^\circ\) slope. The coefficient of static friction between the block and the sloped surface is \(\mu_s = {{params.coef}}\). The block on the slope is connected to a hanging block of mass \(m_h = {{params.mass}} \rm{kg}\) via a massless string that passes over a massless, frictionless pulley. Assume \(g = 9.81 \rm{m/s^2}\).
Part 1#
What is the force of friction acting on the block on the slope \(f\)? Express your answer in terms of the variables in the question.
Note that it may not be necessary to use every variable. Use the following table as a reference for each variable:
For |
Use |
|---|---|
\(m_s\) |
ms |
\(m_h\) |
mh |
\(g\) |
g |
\(\mu_s\) |
mu |
\(\theta\) |
theta |
Answer Section#
Part 2#
What is the tension in the string \(T\)? Express your answer in terms of the variables in the question.
Note that it may not be necessary to use every variable. Use the following table as a reference for each variable:
For |
Use |
|---|---|
\(m_s\) |
ms |
\(m_h\) |
mh |
\(g\) |
g |
\(\mu_s\) |
mus |
\(\theta\) |
theta |
Answer Section#
Part 3#
Use Newton’s second law and your answers to Part 1 and 2 to determine the minimum value of the mass of the block on the slope \(m_s\) such that the system remains at rest.
Answer Section#
Please enter in a numeric value in \(\rm{kg}\).
Attribution#
Problem is licensed under the CC-BY-NC-SA 4.0 license.

