Vehicle Around a Curve

To ensure that motorists stay on roads with tight turns, it is common to tild (or bank) the roads toward the centre of the turn. A semi-truck going around a banked curve without sliding is shown on the left of the figure below and its corresponding free body diagram is shown on the right of the figure below. In the free body diagram \(\vec{W}_{\textit{E on v}}\) is the weight of the semi-truck, \(\vec{n}_{\textit{r on v}}\) is the normal force of the road on the semi-truck, and \(\vec{F}\_{\textit{net on v}}\) is the net force on the semi-truck. Take the angle to be \(\theta = {{ params.ang }}^\circ\) and the radius of curvature (distance from the centre of the circle to the semi-truck) to be \(r = {{ params.rad }}\) \(\rm{m}\).

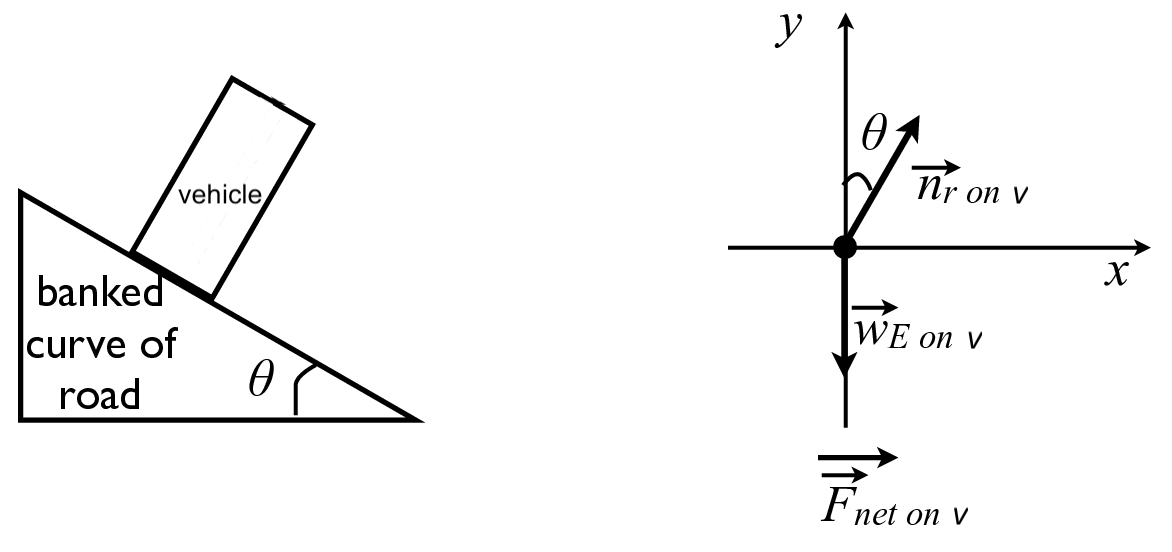
Part 1

Write the equation for Newton’s second law in the \(x\)-direction.

Note that it may not be necessary to use every variable. Use the following table as a reference for each variable:

For	Use
\(W\_{\textit{E on v}}\)	W
\(n\_{\textit{r on v}}\)	n
\(\theta\)	theta

Answer Section

Part 2

Write the equation for Newton’s second law in the \(y\)-direction.

Note that it may not be necessary to use every variable. Use the following table as a reference for each variable:

For	Use
\(W\_{\textit{E on v}}\)	W
\(n\_{\textit{r on v}}\)	n
\(\theta\)	theta

Answer Section

Part 3

Solve the equations in Part 1 and Part 2 algebraically to determine the speed of the semi-truck.

Note that it may not be necessary to use every variable. Use the following table as a reference for each variable:

For	Use
\(m\)	m
\(g\)	g
\(\theta\)	theta
\(r\)	r

Answer Section

Part 4

Determine the speed of the semi-truck.

Answer Section

Please enter in a numeric value in \(\rm{m/s}\)

Attribution

Problem is licensed under the CC-BY-NC-SA 4.0 license.