Box Up Ramp

Box Up Ramp#

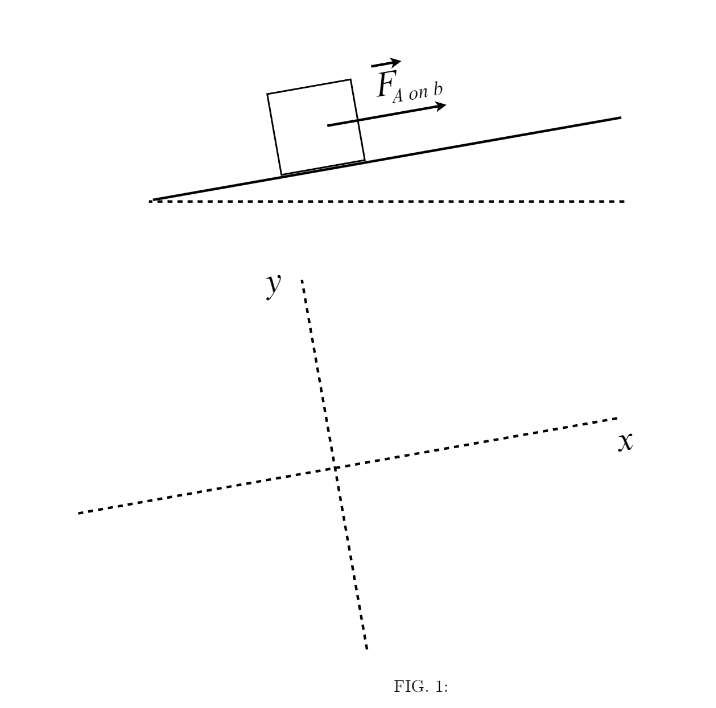
On moving day, Aliyah pushes a box weighing 179.0 \(\rm{N}\) at constant speed up a ramp. They push parallel to the ramp with a force of magnitude \(F\_{\textit{A on B}}\) (see the figure below). The ramp makes an angle of \(\theta = {{params.ang}}^{\circ}\) with the horizontal direction. The coefficients of static and kinetic friction friction between the box and the ramp are \(\mu_s = {{params.s}}\) and \(\mu_k = {{params.k}}\), respectively.

The top diagram is of a box travelling up an inclined ramp. There is a force vector in the center of the box pointing towards the top of the ramp, parallel to the ramp itself. It is labelled $F_{\textit{A on B}}}$. The bottom diagram is of an empty graph whose x-axis is parallel to the ramp while the y-axis is perpendicular to the ramp.

Question Text#

Draw a free body diagram for this problem using the labelled axes provided in the figure. Label each force with subscripts indicating the agent of the force and the force on which it acts. Use R for ramp, A for Aliyah, E for earth, and B for box. Be sure to consider the force Aliyah exerts on the box \(F\_{\textit{A on B}}\), the force of kinetic friction \(f\_{\textit{k, R on B}}\), the force of static friction \(f\_{\textit{s, R on B}}\), the weight of the box \(W\_{\textit{E on B}}\), the normal force \(N\_{\textit{R on B}}\), and any other forces that may be acting on the box.

Answer Section#

File upload box will be shown here.

Part 2#

Is this an example of static or dynamic equilibrium?

Answer Section#

Part 3#

From your free body diagram, write Newton’s second law equation for the x-components.

Note that it may not be necessary to use every variable and for angles, use their numeric value in degrees. Use the following table as a reference for each variable:

For

Use

\(F\_{\textit{A on B}}\)

F_ab

\(f\_{\textit{k, R on B}}\)

F_krb

\(f\_{\textit{s, R on B}}\)

F_srb

\(W\_{\textit{E on B}}\)

W_eb

\(N\_{\textit{R on B}}\)

N_rb

\(\theta\)

theta

Answer Section#

Part 4#

From your free body diagram, write Newton’s second law equation for the y-components.

Note that it may not be necessary to use every variable and for angles, use their numeric value in degrees. Use the following table as a reference for each variable:

For

Use

\(F\_{\textit{A on B}}\)

F_ab

\(f\_{\textit{k, R on B}}\)

F_krb

\(f\_{\textit{s, R on B}}\)

F_srb

\(W\_{\textit{E on B}}\)

W_eb

\(N\_{\textit{R on B}}\)

N_rb

\(\theta\)

theta

Answer Section#

Part 5#

Solve your equations to find \(F\_{\textit{A on B}}\).

Answer Section#

Please enter in a numeric value

Part 6#

If the box started at rest on the ramp, how hard would Aliyah have to initially push the box to just overcome the static force of friction?

Answer Section#

Please enter in a numeric value

Part 7#

Once the box started moving, if Aliyah maintained the force you found in Part 6, what would happen to the box?

Answer Section#

Attribution#

Problem is licensed under the CC-BY-NC-SA 4.0 license.
The Creative Commons 4.0 license requiring attribution-BY, non-commercial-NC, and share-alike-SA license.