Ball Down A Hill

Ball Down A Hill#

A ball, initially at rest, rolls down a hill slanted \(\theta = {{params.theta}}^{\circ}\). After traveling a horizontal distance \(d = {{params.d}} \ \rm{m}\), it moves up a curve whose height follows the equation \(h(x) = \frac{x^2}{2}\).

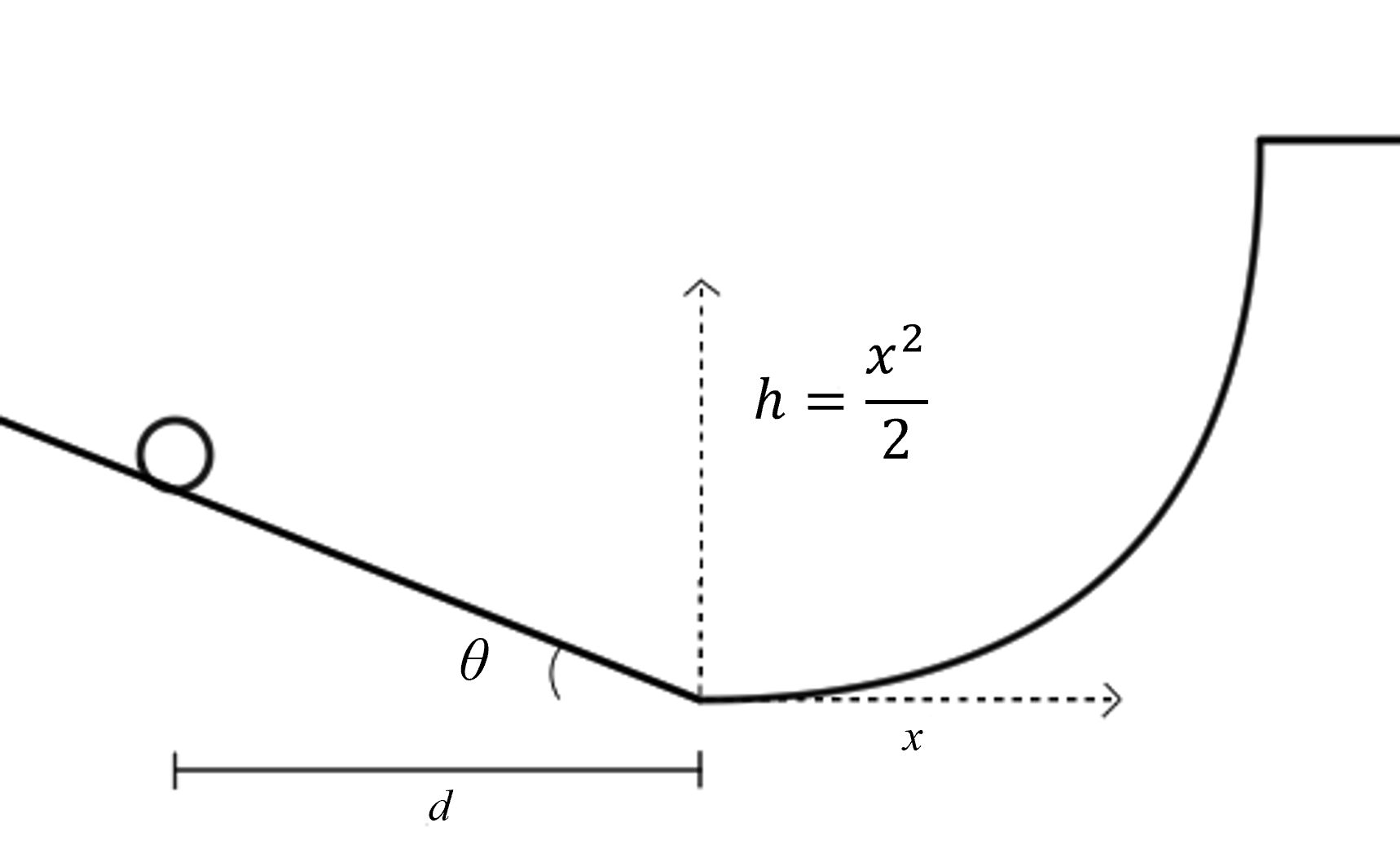
A ball rolls down a hill slanted theta degrees up. At the end of that hill the path curves upwards.

Part 1#

To what height \(h\) does the ball make it up the curve? Neglect friction, and assume a smooth transition from one section to the other.

Answer Section#

Please enter in a numeric value in m.

Part 2#

To what horizontal distance \(x\) does the ball travel from the start of the curve?

Answer Section#

Please enter in a numeric value in m.

Attribution#

Problem is licensed under the CC-BY-NC-SA 4.0 license.
The Creative Commons 4.0 license requiring attribution-BY, non-commercial-NC, and share-alike-SA license.