Spring Oscillator

Spring Oscillator#

A wooden train is attached to two linear springs of spring constant \(k\) in a closed box. The train is displaced from the center of the box by \(x_0 \ \rm{m}\).

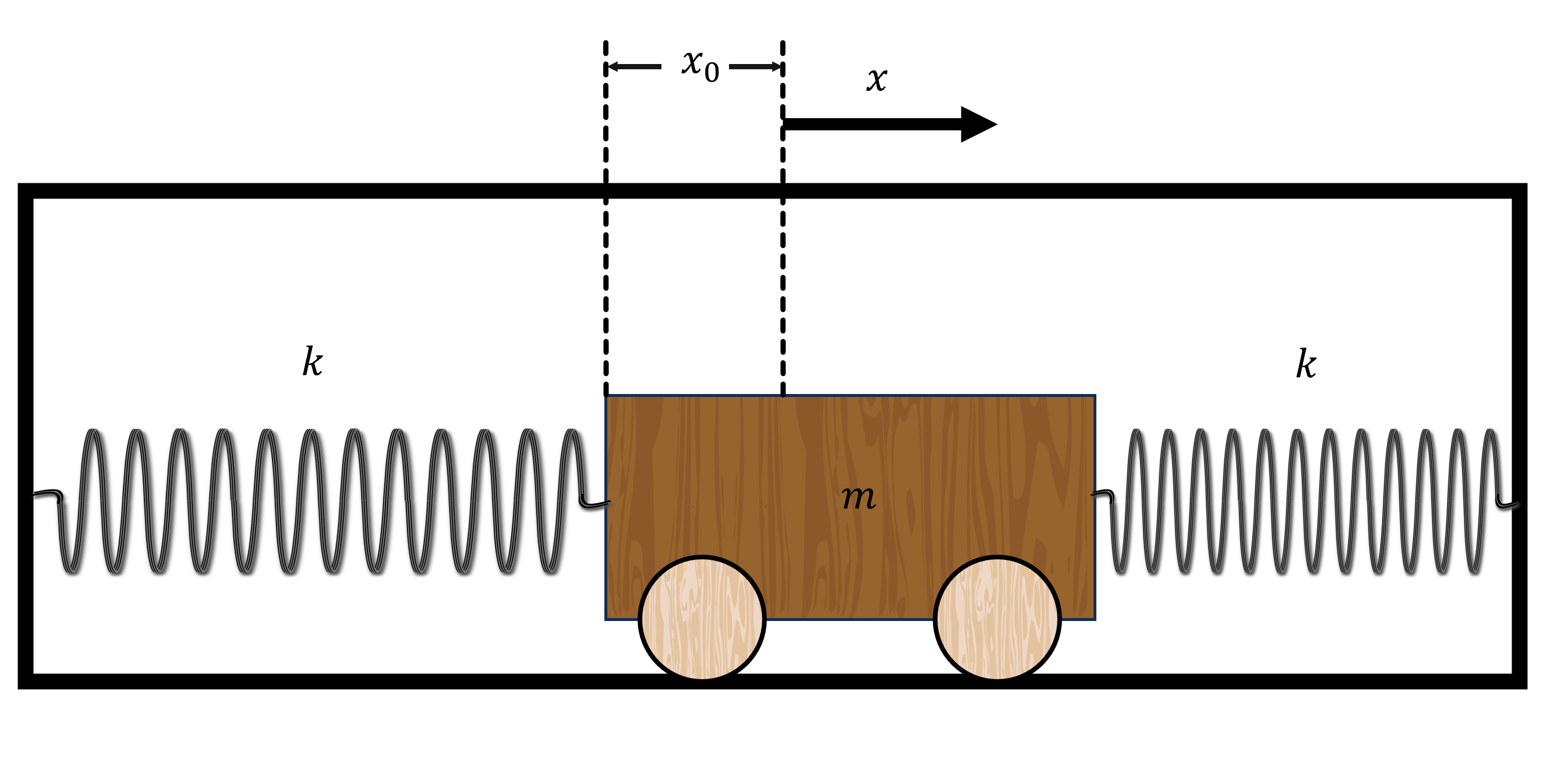
../../../../../_images/part19.png

Part 1#

If the train is released from rest and it moves along the frictionless floor, what is the total force in the x-direction acting on the train at the point of release?
\(m= {{ params.m }} \ \rm{kg}\), \(x\_{0}= {{ params.x_0 }} \ \rm{cm}\), \(k = {{ params.k }} \ \rm{N/m}\).

Answer Section#

Please enter in a numeric value in \(N\).

Part 2#

What is the maximum acceleration of the train?

Answer Section#

Please enter in a numeric value in \(ms^{-2}\).

Part 3#

By obtaining the displacement of the train as a function of time, determine the period of oscillation of the train i.e the time that it takes for the train to return back to its starting position.

Answer Section#

Please enter in a numeric value in \(s\).

Part 4#

If the spring stiffness constant is quadrupled, what is the new period of oscillation?

Answer Section#

Please enter in a numeric value in \(s\).

Attribution#

Problem is licensed under the CC-BY-NC-SA 4.0 license.
The Creative Commons 4.0 license requiring attribution-BY, non-commercial-NC, and share-alike-SA license.