Rope Tension Between Blocks#
As pictured, two blocks of mass \(2m\) are connected by a rope of tension \(T_3\) and pulled along a frictionless surface. Another (massless) rope of tension \(T_2\) connects the two blocks to a (frictionless) pulley of mass \(m/2\), which is a disk of radius \(R\). The (massless) rope continues with tension \(T_1\) on the other side of the pulley to a hanging mass of mass \(m\).
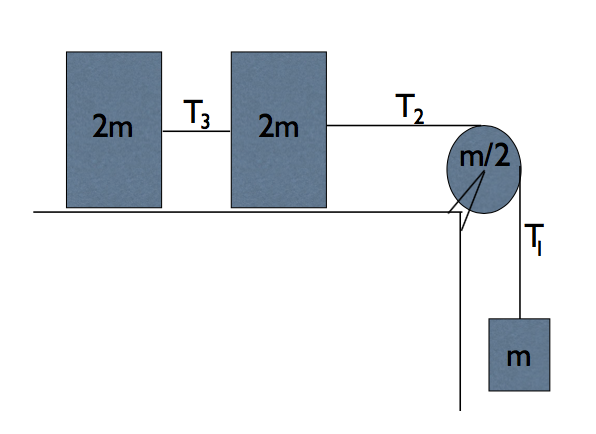
Part 1#
Referring to the image, the tensions in the ropes satisfy:
Answer Section#
\(T_3\) > \(T_2\) > \(T_1\)
\(T_3\) > \(T_2\) = \(T_1\)
\(T_3\) = \(T_3\) = \(T_1\)
\(T_3\) < \(T_2\) < \(T_1\)
\(T_3\) < \(T_2\) = \(T_1\)
Part 2#
Referring to the image, the magnitude of the acceleration of the system is:
Answer Section#
\(a = \frac{4}{21} g\) \(\rm{ \frac{m}{s^2} }\)
\(a = \frac{g}{4}\) \(\rm{ \frac{m}{s^2} }\)
\(a = \frac{g}{2}\) \(\rm{ \frac{m}{s^2} }\)
\(a = g\) \(\rm{ \frac{m}{s^2} }\)
\(a = \frac{2}{3} g\) \(\rm{ \frac{m}{s^2} }\)
Attribution#
Problem is licensed under the CC-BY-NC-SA 4.0 license.

