Particle Energy to Force Diagram#
Question Text#
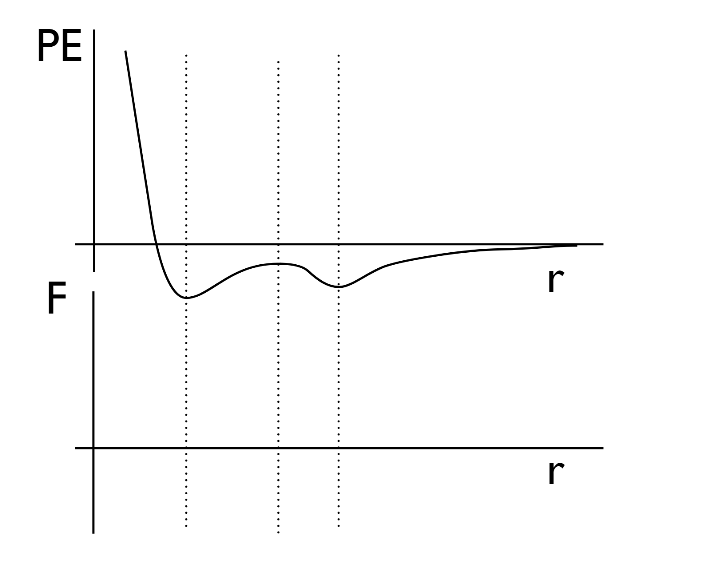
The potential energy of a particle in a conservative potential is shown below in Fig. 1. Sketch the force diagram as a function of radius for this particle. Save the diagram and use the provided dashed lines to guide your diagram.
Please upload the final diagram as a pdf titled “diagram.pdf”.
Answer Section#
File upload box will be shown here.
Attribution#
Problem is licensed under the CC-BY-NC-SA 4.0 license.

