Cat in a Laundry Basket#
A cat jumps out of a laundry basket, travelling \(w = \) 26 \(cm\) horizontally before just clearing the \(h =\) 33 \(cm\) high edge of the basket. The parabolic trajectories of three different jumps labelled 1, 2, and 3 are shown below.
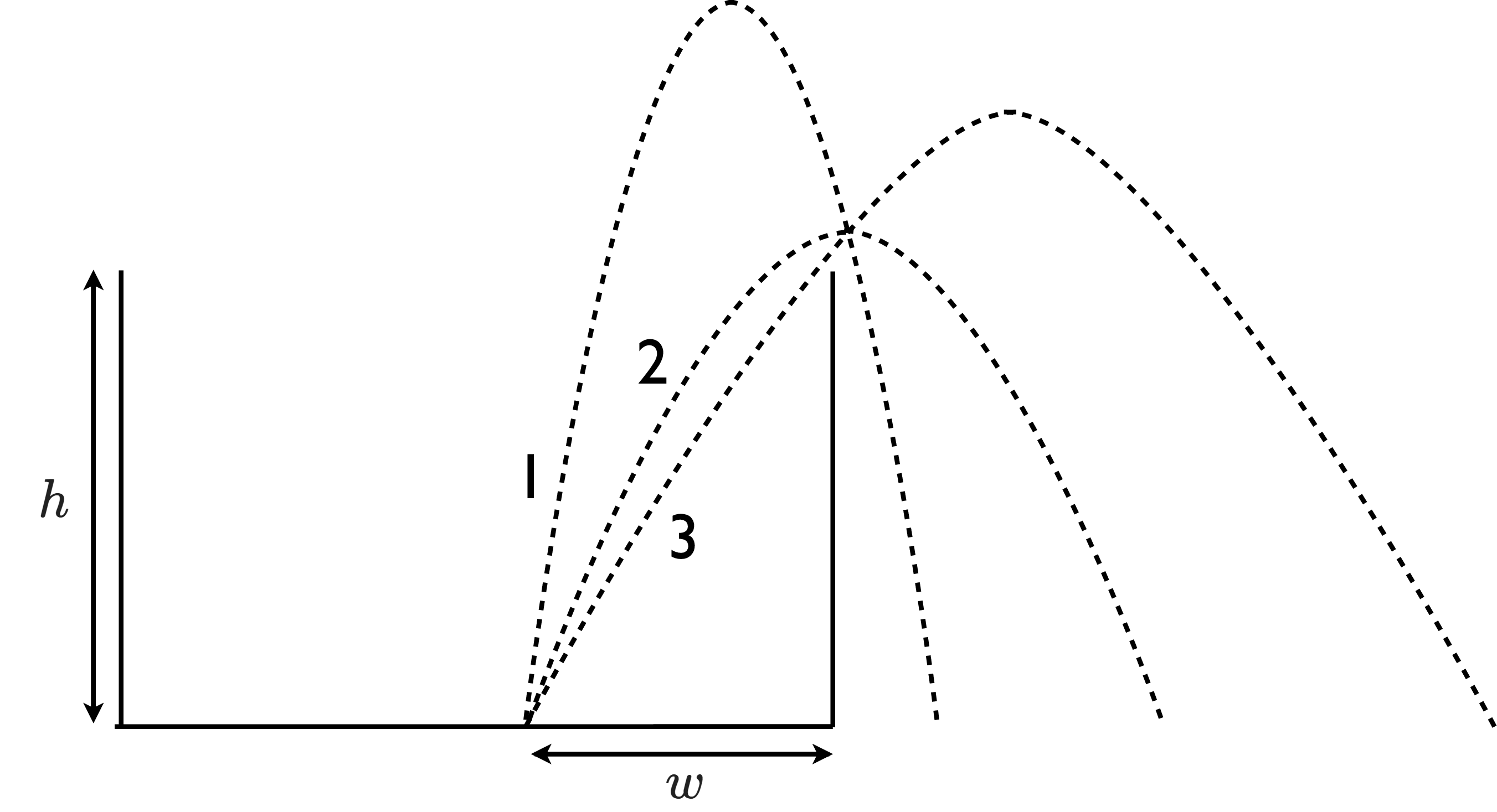
Long Description of image: The parabolic trajectories of three different jumps.
Trajectory 1 has the highest peak and smallest range.Trajectory 2 has the lowest peak and the second largest range.
Trajectory 3 has the second highest peak and the largest range.
Long description ends.
Part 1#
Rank the time in the air (\(\Delta t_1, \Delta t_2, and \Delta t_3\), respectively) of the cat on each path.
Answer Section#
\(\Delta t_1 > \Delta t_2 > \Delta t_3\)
\(\Delta t_1 > \Delta t_3 > \Delta t_2\)
\(\Delta t_2 > \Delta t_1 > \Delta t_3\)
\(\Delta t_2 > \Delta t_3 > \Delta t_1\)
\(\Delta t_3 > \Delta t_1 > \Delta t_2\)
\(\Delta t_3 > \Delta t_2 > \Delta t_1\)
Part 2#
Rank the relative sizes of the \(x-\)components of the velocity vectors for path 1 (\(v\_{x1}\)) and path 2 (\(v\_{x2}\)).
Answer Section#
\(v_{x1} > v_{x2}\)
\(v_{x2} > v_{x1}\)
\(v_{x1} = v_{x2}\)
Attribution#
Problem is licensed under the CC-BY-NC-SA 4.0 license.

