Position XY 1b

Position XY 1b#

Part 1#

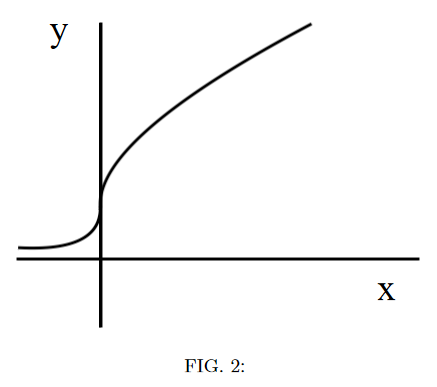
A particle follows the trajectory shown in the figure without stopping along it’s path. What can you conclude aboout the particle’s motion?

An image showing a particle's trajectory on a cartesian plane (x versus y). For negative x-coordinates, the particle follows a concave up trajectory with positive y-coordinates. At the y-axis, the particles trajectory is parallel to the y-axis. For positive x-coordinates, the particle follows a concave down trajectory with positive y-coordinates.

Answer Section#

  • At \(x = 0\), the particle’s instantaneous velocity points in either the \(\hat{\imath}\) or the \(-\hat{\imath}\) direction.

  • At \(x = 0\), the particle’s instantaneous velocity points in either the \(\hat{\jmath}\) or the \(-\hat{\jmath}\) direction.

  • At \(x = 0\), the particle’s instantaneous acceleration is zero.

  • At \(x = 0\), the particle’s instantaneous acceleration non-zero.

  • No information about the particle’s velocity or acceleration can be found from its trajectory.

Attribution#

Problem is licensed under the CC-BY-NC-SA 4.0 license.
The Creative Commons 4.0 license requiring attribution-BY, non-commercial-NC, and share-alike-SA license.