Mass inside a Rotating Cone#
Question Text#
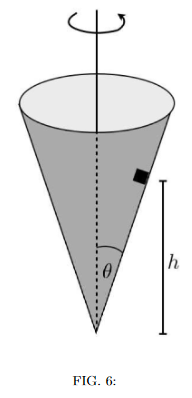
As shown in the figure, a small block of mass \(m\) is placed inside an inverted cone. The mass is put into rotational motion around the inside of the cone around a vertical axis with period \(T\). The walls of the cone can be assumed to be frictionless, and make an angle \(\theta\) with the vertical. What is the value of \(T\) if the block is to remain at a height \(h\) above the apex of the cone? Give your answer for \(T\) in terms of \(m\), \(h\), \(g\), and \(\theta\).
Note that it may not be necessary to use every variable. Use the following table as a reference for using each variable:
For |
Use |
|---|---|
\(m\) |
m |
\(h\) |
h |
\(g\) |
g |
\(\theta\) |
theta |
Answer Section#
Attribution#
Problem is licensed under the CC-BY-NC-SA 4.0 license.

