Wheel of Fortune#
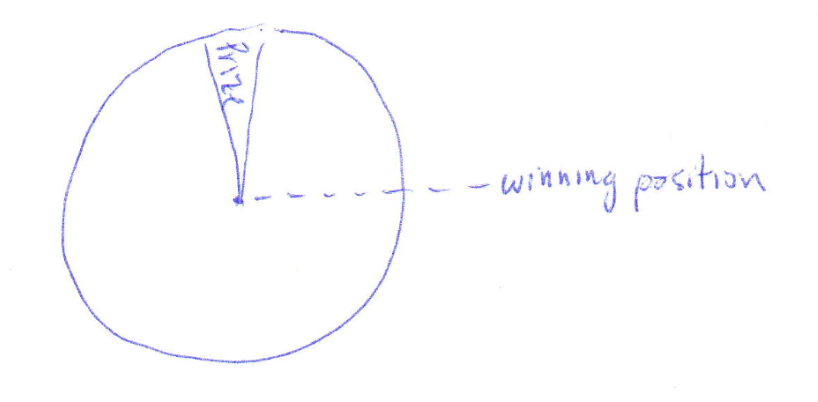
Lorenzo wants to win a game of Wheel-of-Fortune. The grand prize is located at a position at the top of the wheel when each contestant spins the wheel. Contestants win the prize located at the position to the right when the wheel stops (shown below). Lorenzo notes that when another contestant set the wheel spinning at \(\omega_i = \) \({\pi \over 2} {rad\over s}\) in the counter-clockwise direction, it takes 1.9 \(s\) to stop.
Part 1#
With which initial velocity in the counter-clockwise direction should Lorenzo spin the wheel to win the grand prize? Note that it is not possible to spin the wheel such that it undergoes more than 16 full rotations. Your answer should include three significant figures.
Answer Section#
Please enter in a numeric value in rad/s.
Attribution#
Problem is licensed under the CC-BY-NC-SA 4.0 license.

