Elevator Pulley System#
A \(m = {{ params.m_p }} \rm{kg}\) person in a \(M = {{ params.M_e }} \rm{kg}\) elevator lifts themselves at constant velocity by pulling on the rope shown in the figure below. The rope passes over a pulley attached to the top of the elevator shaft, back over a pulley attached to the top of the elevator, over a second pulley attached to the top of the elevator shaft, and attaches to the top of the elevator. Treat the rope as if it is massless and the pulleys as if they are frictionless and massless. At the instant shown in the figure below, the rope passing over the elevator’s pulley makes a \(\theta = {{ params.ang }}^\circ\) angle with the vertical.
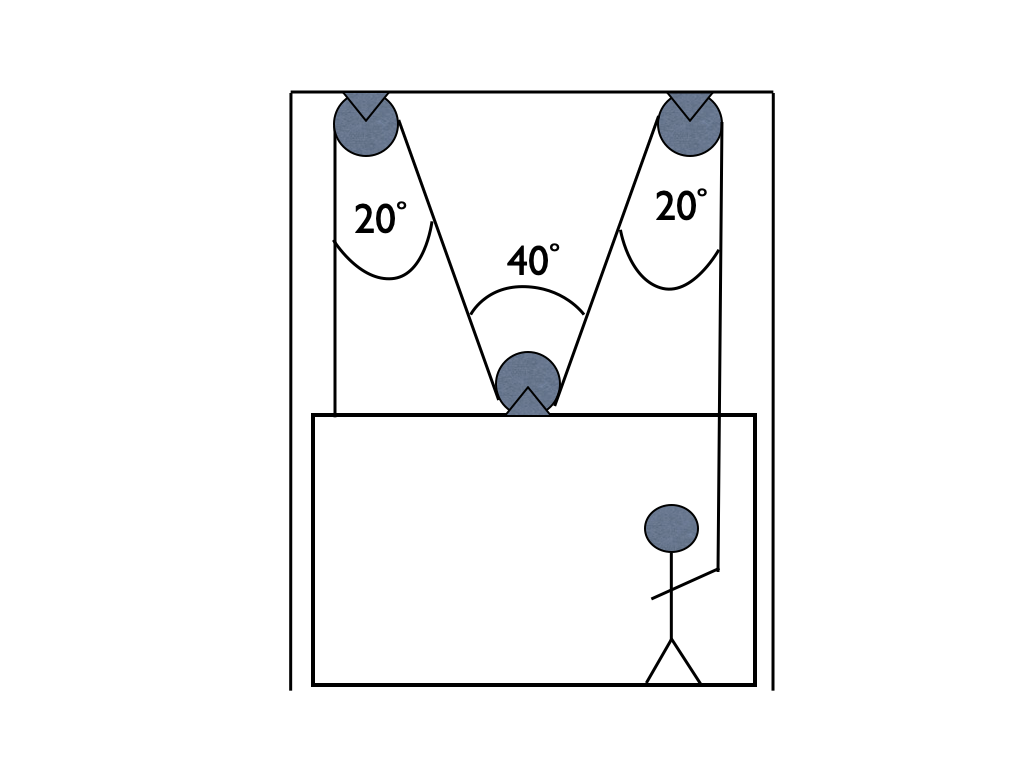
Part 1#
Should the tension in the rope be the same in all portions of the rope?
Answer Section#
{‘value’: ‘Yes’}
{‘value’: ‘No’}
Part 2#
Explain your answer to Part 1.
Answer Section#
Answer in 1-2 full sentences.
Part 3#
Draw force identification diagrams for the elevator and the person.
Be sure to label the weight of the person \(mg\), the weight of the elevator \(Mg\), the tension \(T\), the normal force of the person acting on the elevator \(n\_{\text{pe}}\), and the normal force of the elevator acting on the person \(n\_{\text{ep}}\).
Save your force identification diagrams as “fid.pdf” and upload the file below.
Answer Section#
File upload box will be shown here.
Part 4#
Draw free body diagrams for the elevator and the person.
Be sure to label the weight of the person \(mg\), the weight of the elevator \(Mg\), the tension \(T\), the normal force of the person acting on the elevator \(n\_{\text{pe}}\), and the normal force of the elevator acting on the person \(n\_{\text{ep}}\). Specify the net force beside your diagrams.
Save your free body diagrams as “fbd.pdf” and upload the file below.
Answer Section#
File upload box will be shown here.
Part 5#
Write Newton’s second law in the vertical direction for the elevator.
Note that it may not be necessary to use every variable. Use the following table as a reference for using each variable:
For |
Use |
|---|---|
\(m\) |
m |
\(M\) |
M |
\(\theta\) |
theta |
\(T\) |
T |
\(g\) |
g |
\(n\_{\text{pe}}\) |
n_pe |
\(n\_{\text{ep}}\) |
n_ep |
Answer Section#
Part 6#
Write Newton’s second law in the vertical direction for the person.
Note that it may not be necessary to use every variable. Use the following table as a reference for using each variable:
For |
Use |
|---|---|
\(m\) |
m |
\(M\) |
M |
\(\theta\) |
theta |
\(T\) |
T |
\(g\) |
g |
\(n\_{\text{pe}}\) |
n_pe |
\(n\_{\text{ep}}\) |
n_ep |
Answer Section#
Part 7#
Which two forces are related by Newton’s third law?
Answer Section#
Select all the choices that apply.
Note: You will be awarded full marks only if you select all the correct choices, and none of the incorrect choices. Choosing incorrect choices as well as not choosing correct choices will result in deductions.
\(T\)
\(n_{ep}\)
\(Mg\)
\(mg\)
\(n_{pe}\)
Part 8#
Are the two forces identified in Part 8 on the same free body diagram?
Answer Section#
{‘value’: ‘Yes’}
{‘value’: ‘No’}
Part 9#
Solve the equations in Part 5 and Part 6 for the tension in the rope.
Answer Section#
Please enter in a numeric value in \(\rm{N}\).
Part 10#
Solve the equations in Part 5 and Part 6 for the apparent weight of the person as measured by a scale under their feet while they are pulling up on the rope.
Answer Section#
Please enter in a numeric value in \(\rm{N}\).
Attribution#
Problem is licensed under the CC-BY-NC-SA 4.0 license.

