Cricket Wicket By Catch#
In a game of cricket akin to baseball, a batsman returns the ball bowled on a pitch and scores runs based on the distance travelled by the ball upon exiting the collision with the bat.
Part 1#
If the ball leaves the bat with a speed of \(u\ \rm{m/s}\) at an angle \(\alpha\) measured up from the horizontal as shown in the image below, determine the value of $\( \dot{R} \)\( in \)\rm{m/s}$ as observed by a stationary spectator.
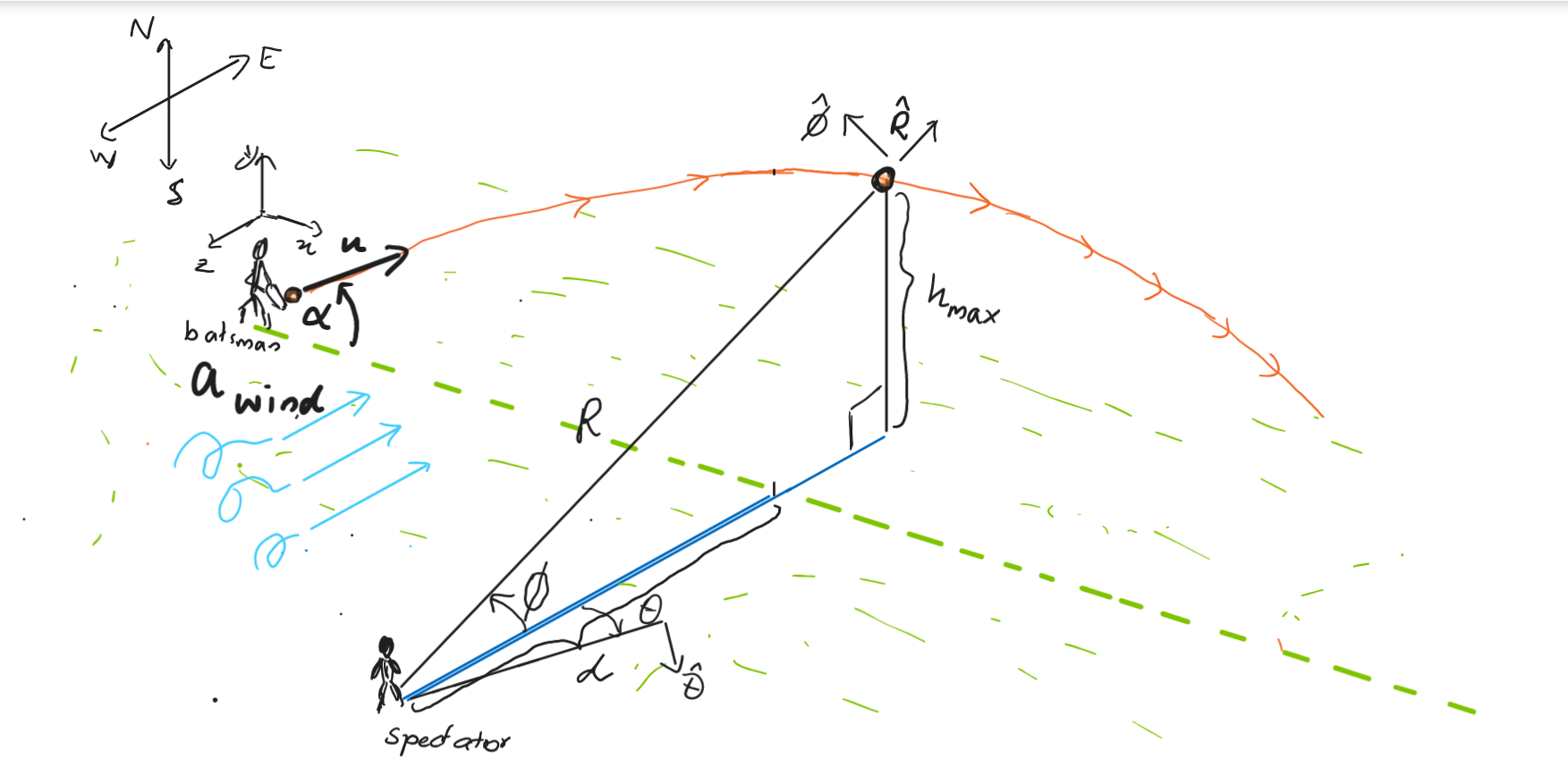
Treat the ball as a particle and assume an east-ward acceleration awind acting on the ball due to the wind.
\(\alpha = {{ params.a }}^\circ\), \(u = {{ params.u }}\ \rm{m/s}\), \(d = {{ params.d }}\ \rm{m}\), \(a\_{wind} = {{ params.a_w }}\ \rm{m/s^{2}}\).
Answer Section#
Please enter in a numeric value in m/s.
Part 2#
Determine the value of $\( \dot{\phi} \)$.
Answer Section#
Please enter in a numeric value in rad/s.
Part 3#
Determine the value of $\( \dot{\theta} \)$.
Answer Section#
Please enter in a numeric value in rad/s.
Part 4#
Determine the value of $\( \ddot{R} \)$.
Answer Section#
Please enter in a numeric value in \(ms^{-2}\).
Part 5#
Determine the value of $\( \ddot{\theta} \)$.
Answer Section#
Please enter in a numeric value in \(rads^{-2}\).
Part 6#
Determine the value of $\( \ddot{\phi} \)$.
Answer Section#
Please enter in a numeric value in \(rads^{-2}\).
Attribution#
Problem is licensed under the CC-BY-NC-SA 4.0 license.

