The Capacitor#
# Additional styling ; should be moved into helpers
from IPython.core.display import display, HTML
HTML('<style>{}</style>'.format(open('styler.css').read()))
Welcome!#
To run a cell, click the cell and hit “Shift+Enter” on your keyboard.
from helpers import *
Reminder & Review!#
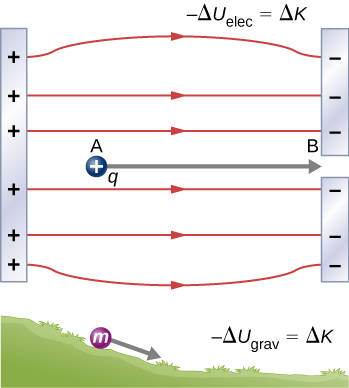
Electric fields \(\vec{E}\) are formed between positive and negative charges
\(\vec{E}\) has magnitude (units of \(N/C\) or \(V/m\)) and a direction
The work done on a charge \(q\) by the electric field is:
The voltage difference between two plates can be expressed as:
Learning Objectives#
Identify and summarize key functions of the capacitor
Explain the relationship between the capacitance and the plate separation and area
Describe applications of the capacitor based on its properties
Stud finder!#
Today you will learn how a stud-finder works - it uses electric fields and a capacitor!
IFrame(stud_finder,width='100%',height=600)
What is a capacitor?#
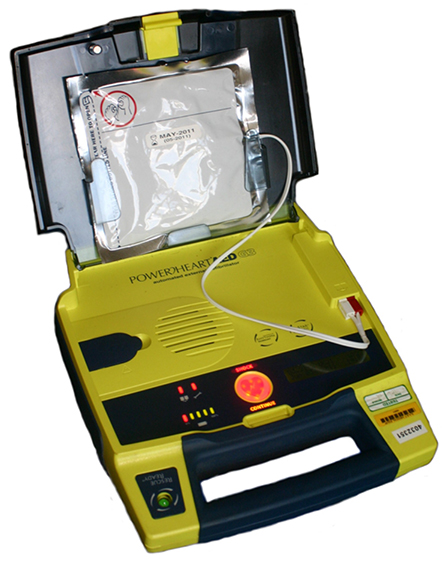
Capacitors are very important components of many electronic devices including:
Pacemakers
Flash lamps on cameras
Defribrillators
Cell phones and computers
A capacitor is a device that stores electrical charge.
The energy is stored within an electric field (between two conducting plates).
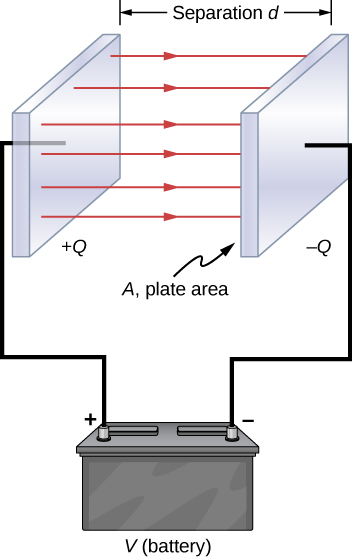
Capacitance is defined as the ratio of the charge \(Q\) on a conductor to the potential difference \(V\) between them:
On the right, is the parallel plate capacitor.

The unit of capacitance is a “Farad”, or F (in honour of Michael Faraday)
Exploring Capacitors#
We will explore the dependence of three parameters on the capacitance:
Voltage \(V\)
Plate separation \(d\)
Plate area \(A\)
We will use a simulation app to build and develop some intuition!
display(Markdown("## Capacitor Simulation Demo"))
IFrame(capacitor_phet, width='100%',height=900)
Capacitor Simulation Demo
Activity 1: Does the battery affect the Capacitance?#
What do you think happens to the Capacitance if:
the battery voltage is maximum ?
the battery voltage is 0 ?
the battery voltage is negative?
IFrame('https://app.sli.do/event/gkmj65xm/embed/polls/43a660b4-f549-4cde-b9b3-91165a66a42a', width=700,height=500)
IFrame(capacitor_phet, width='100%',height=600)
Instructions#
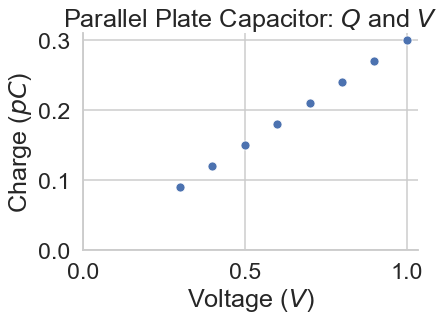
Keep all parameters except the Voltage constant.
Step through the voltages from 0.3 to 1.0 in units of 0.1 V and record the top-plate charge.
Type in the data for V and Q into the lists below.
Observe the relationship between Voltage (\(V\)) and Charge (\(Q\)) in the plot.
voltage = [0.30, 0.40, 0.50, 0.60, 0.70, 0.80, 0.90, 1.0] # units: V
charge = [0.09, 0.12, 0.15, 0.18, 0.21, 0.24, 0.27, 0.30] # units: pC
# Plot here
plot_VQ(voltage,charge)
Activity 2: Effect of plate separation on capacitance#
What do you think happens to the \(\vec{E}\) field when:
the plates touch (\(d = 0\)) ?
the plates are extremely far apart (\(d \to \infty\)) ?
IFrame('https://app.sli.do/event/gkmj65xm/embed/polls/07567c0d-6ab5-4a01-a7e6-ec99cf8c8eaf', width=700,height=500)
IFrame(capacitor_phet, width='100%',height=600)
Instructions#
Keep all parameters except the plate separation constant.
Charge the capacitor (set \(V\) to 1.5V).
Step through at least 6 separation distances between 2.0 mm to 10mm and record the Capacitance.
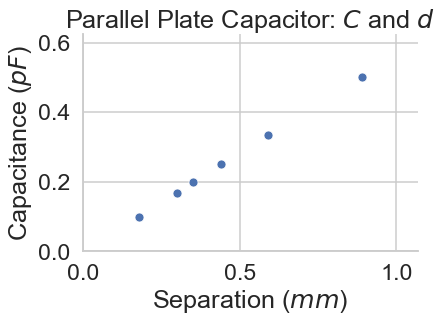
Type in the data for capacitance and separation into the lists below.
Identify the relationship between \(C\) and \(d\).
capacitance = [0.18, 0.30, 0.35, 0.44, 0.59, 0.89] # units: pF
separation = [1/10, 1/6.0, 1/5.0, 1/4.0, 1/3.0, 1/2.0] # units: mm
# Plot here
plot_dC(capacitance,separation)
Activity 3: Effect of plate area on capacitance#
What do you think happens to the charges when:
the plate area A increases, \(A\to \infty\) ?
the plate area A decreases, \(A \to 0\) ?
IFrame('https://app.sli.do/event/gkmj65xm/embed/polls/6881fa0b-2c6f-4f38-aaae-967d10c8129e', width=700,height=500)
IFrame(capacitor_phet, width='100%',height=600)
Instructions#
Keep all parameters except the plate area constant.
Step through at least 4 areas between 100 and 400 mm\(^2\) and record the Capacitance.
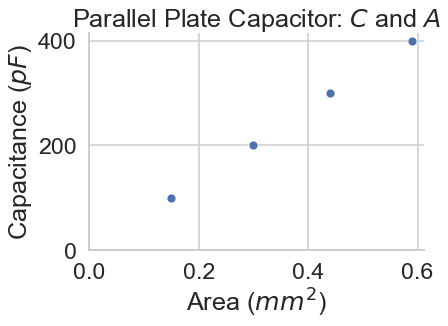
Type in the data for capacitance and areas into the lists below.
Identify the relationship between \(C\) and \(A\).
capacitance = [0.15, 0.30, 0.44, 0.59 ] # units: pF
area = [100,200,300,400 ]# units: mm^2
plot_AC(capacitance,area)
Recap: Parallel Plate Capacitor Activity#
C and Voltage \(V\):
C and Plate separation \(d\):
C and Plate area \(A\):
Capacitance of a Parallel Plate Capacitor:#
$\( C = \frac{\epsilon_0 A}{d} \)\(
<br><br><br><br><br>
Where does \)\epsilon_0$ come from? Go back to this pencast for the derivation of the Electric Field between parallel plates. More in the Tutorial this week!
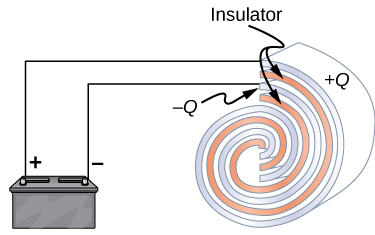
Capacitors in practice#
Capacitors come in many shapes and geometries:

Typically an insulating material is placed between conducting sheets (dielectric) to make the capacitor more effective
Between the plates#
This is a molecular model of an insulating material that contains polar (one side positive, one side negative) molecules:

Notice that the molecules are currently randomly assorted and distributed.
If an electric field is applied across an insulator (for e.g., when placing this material between the plates of a capacitor), individual molecules become aligned with the electric field.
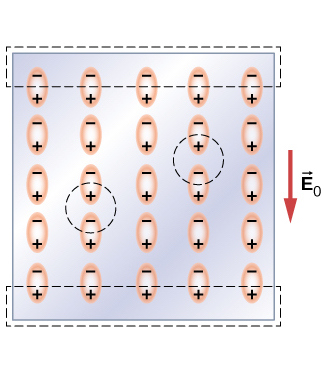
Thus, the main electric field \(E_0\) is “reduced” by the electric field in the opposite direction \(E_i\) induced by the dielectric material.

Reducing of the electric field results in a DECREASE in voltage (\(V = E\cdot d\)), and consequently, an INCREASE in capacitance (\(C=Q/V\)) since the charge Q on the plates is constant.
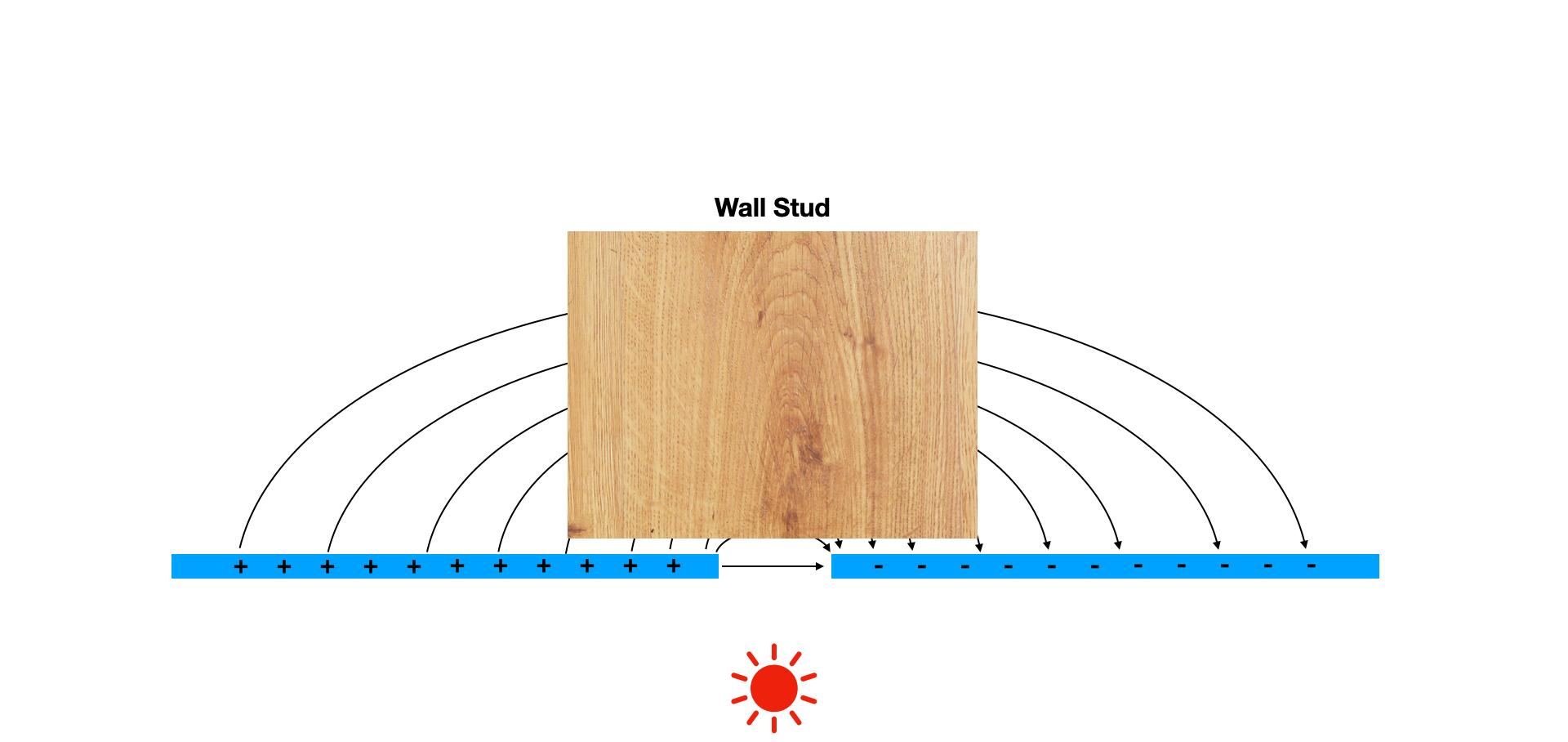
Back to the Studfinder#
Now you have all the physics and intuition you need to work out how a stud finder works (hint: it uses capacitance and dielectrics)!
There is just one more key piece of insight, but it’s “geometry”…

Instructions: In break-out rooms, discuss and see if you can figure out how the stud finder works!#
Watch the magic (geometry)!#

Stud Finder#
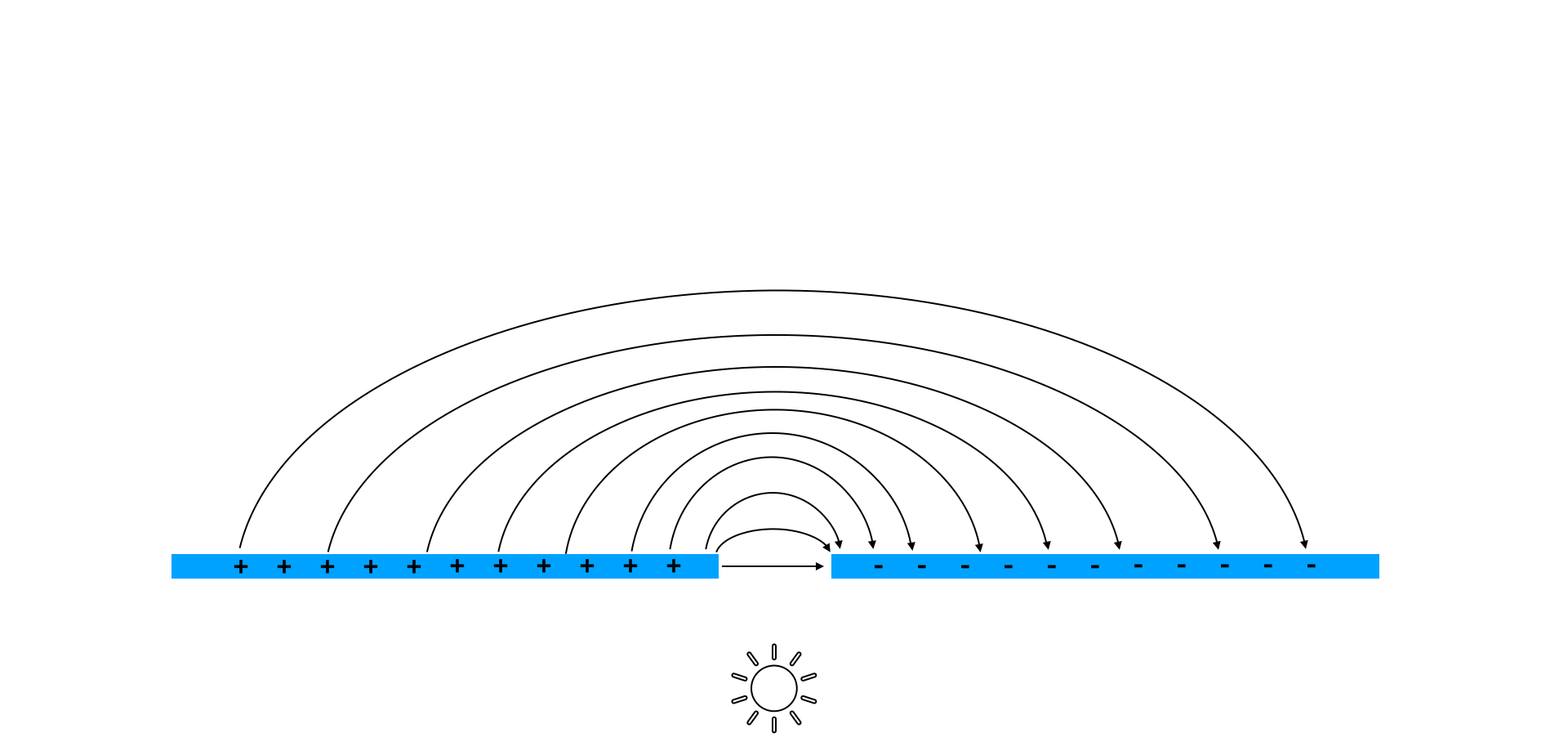
Stud Finder#
Challenge Question#
IFrame(capacitor_phet, width='100%',height=550)
Let’s disconnect the battery, and then observe the voltage \(V\) across the parallel plates after we decrease the plate separation \(d\) and increase the plate area \(A\).
Question: Can you explain how the voltage across the capacitor can be larger than the initially supplied voltage? Answer in 3-4 sentences.
Recap Learning Objectives#
Identify and summarize key functions of the capacitor
Capacitors store and release energy in a controlled manner
Energy is stored within the electric field
Explain the relationship between the capacitance and the plate separation and area
\(C\) is inversely proportional to plate separation \(d\)
\(C\) is proportional to plate area \(A\)
Describe applications of the capacitor based on its properties
Defribrillator: Controlled storage and release of energy
Stud finder: plates are planar and the stud (different dielectric) changes the capacitance
Post-lecture Conceptual Questions#
qs = display(Q1), display(Q2), display(Q3), display(Q4), display(Q5)
Next class#
Quantifying the energy stored in a capacitor
Dielectric constant \(\kappa\) of different materials
Adding capacitors in series and parallel
Reminder: In Tutorial this week, you will work through the derivation of the Capacitance in a parallel plate capacitor!
Have a great week!#
Appendix#
Deriving the E field within parallel plates using Gauss’ Law#
### Gauss' Law Derivation
IFrame('https://www.youtube-nocookie.com/embed/gTfEFwVsgKA', width=700,height=400)

