Blood types

Blood types#

	AC	B	AB	O
Rh positive	${{ params.a_pos }}$	${{ params.b_pos }}$	${{ params.ab_pos }}$	${{ params.o_pos }}$
Rh negative	${{ params.a_neg }}$	${{ params.b_neg }}$	${{ params.ab_neg }}$	${{ params.o_neg }}$

A person with type O blood and a negative Rh factor can donate blood to any blood type. We define the following events:

A and O are mutually exclusive (since it is impossible for a person to have both bloodtypes)
Events A and E are not mutually exclusive (since 6% of population have blood type A and a postive Rh, that is $P(A\cap E) \neq 0$)
Events E and F are compliments since
$P(E) + P(F) = 1$
$P(E) = 1 - P(F)$
$ {{ params.a_pos }} + {{ params.b_pos }} + {{ params.ab_pos }} + {{ params.o_pos }} = 1 - ({{ params.a_neg }} + {{ params.b_neg }} + {{ params.ab_neg }} + {{ params.o_neg }} )$
${{ params.lh }} = 1 - {{ params.rh }}$

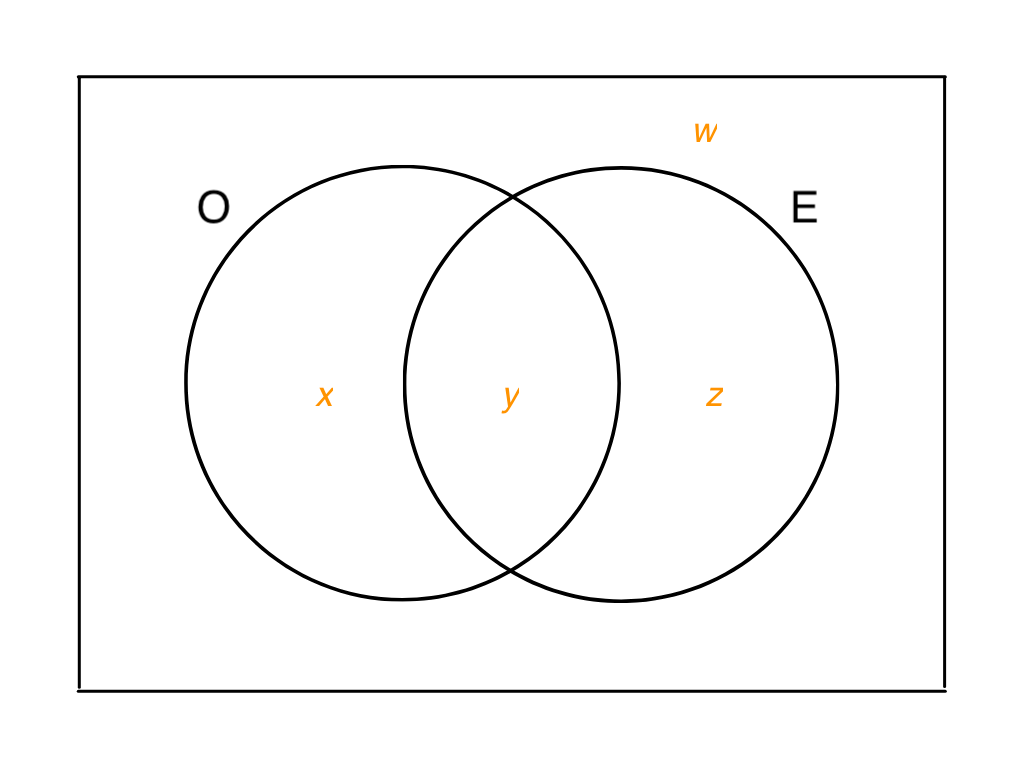
Round all answers to 3 decimal places.